Fast (Matrix) Exponentiation in R

A few days ago, Eric published the blog post titled "Taking powers of a matrix in R". It's quite a nice post, and certainly re-introduces me to some linear algebra which I may have once known. Who can say.

Let's say want to raise a matrix M to some power k (exponentiation). Because I got annoyed with unicode superscripts, I'm going to use the notation pow(M, k) for this.

Eigenvalues For The Win!

Eric's (cute) observation is that we can decompose a matrix M into a diagonal form PDP⁻¹; then pow(M, k) is P(pow(D, k))P⁻¹. Since D is diagonal, it's far faster to exponentiate it than a general matrix.

Eric discusses one drawback to this approach:

• only better for large n (n > 80)

There are a couple of other drawbacks:

• complex arithmetic (for real or integer matrixes);
• not exact for integer inputs;
• not actually very fast.

Repeated Squaring tho

The fast way is repeated squaring. To take an example: pow(M, 8) is M-squared-squared-squared. Instead of 8 (or 7) multiplications, we can use 3 squarings (which is 3 multiplications).

So, a bit more formally:

pow(M, 2*n) is square(pow(M, n));

pow(M, n+1) is M*pow(M, n).

This leads to a recursive scheme to raise a matrix M to the nth power. It has two recursive cases, one when n is even (n is halved), one when n is odd (n is reduced by one). Both of these reduce n, so eventually we hit the base case, which is that pow(M, 0) is I.

In R code:

pow_sq_recursive = function (A, k) {
  if(k == 0) {
    # identity
    diag(1, nrow(A))
  } else if(k %% 2 == 1) {
    A %*% pow_sq_recursive(A, k-1)
  } else {
    pow_sq_recursive(A %*% A, k %/% 2)
  }
}

(I couldn't avoid also writing the true iterative version of this function, see the github repo for details)

Repeated squaring is a lot faster

I have shamelessly stolen Eric's code to produce a retread of his lovely graph:

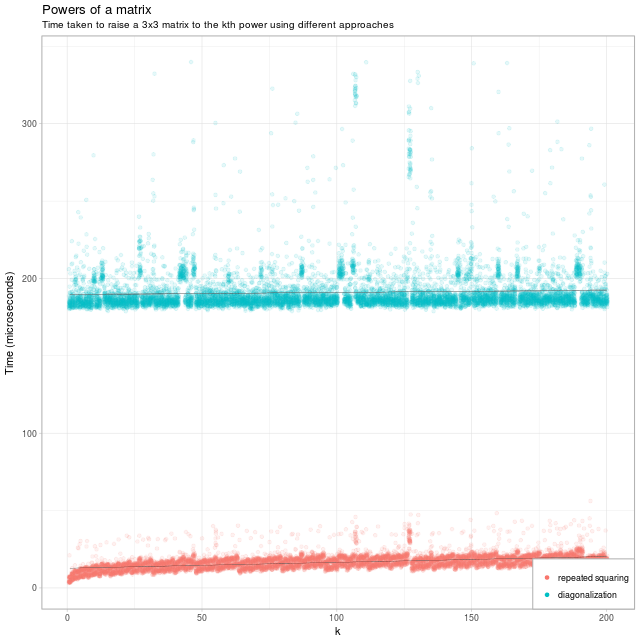
So, we can certainly see that repeated squaring is a lot faster than diagonalisation.

Eric reckons that 82 matrix multiplications take about the same time as the diagonalisation method. The repeated square method has O(log k) growth; it uses 82 matrix multiplications for k between pow(2, 42) (4 trillion, or 4e12) and pow(2, 82) (5 septillion, or 5e24).

So when computing pow(M, k) you should switch from naive linear multiplication to diagonalisation at about k = 82; with repeated squaring you can go a bit further, I estimate switching at k well above 4 trillion.

Repeated squaring is textbook stuff

It's worth noting that the repeated squaring algorithm applies to any situation where we can use multiplication. So we can use it for ordinary numbers, polynomials (useful for increment recomputation of Cyclic Redundancy Check polynomials), finite groups, and of course matrixes.

I'm actually not sure how obscure this "repeated squaring" technique is, but it's in Chapter 1 of my favourite book, Structure and Interpretation of Computer Programs. It's also required on any crypto course, because various crypto algorithms involve raising numbers (in finite groups) to large powers.

But What About R?

But surely this is all silly? We shouldn't be writing blog posts about how to efficiently exponentiate in R, because R already has sensible builtins that use well understood and efficient algorithms.

Doesn't it?